Режимы шифрования

Олег Зензин,

Вступление

В данном материале разъясняется что такое режимы шифрования и какими они бывают. Описание пяти основных режимов шифрования приводится на основании документа, изданного Американским Национальным Институтом Стандартов и Технологий (сокращённо НИСТ). Предполагается, что читатель представляет себе, что такое блочный шифр, но не более того. То есть для понимания материала не требуется знания какого-либо блочного шифра или каких-либо других знаний по криптографии. В этом смысле материал в известной степени самодостаточен. Однако интересующимся могу порекомендовать среди прочих замечательный веб-сайт Андрея Винокурова посвящённый блочным шифрам и криптографии вообще.

Соглашения и термины

Прежде всего необходимо дать определение, что такое режим шифрования и какие в связи с этим понятия или термины нам придётся ввести. Под режимом шифрования здесь понимается такой алгоритм применения блочного шифра, который при отправке сообщения позволяет преобразовывать открытый текст в шифротекст и, после передачи этого шифротекста по открытому каналу однозначно восстановить первоначальный открытый текст. Как видно из определения сам блочный шифр теперь является лишь частью другого алгоритма – алгоритма режима шифрования. Это обусловлено тем, что блочный шифр работает только с отдельным блоком данных, в то время как алгоритм режима шифрования имеет дело уже с целым сообщением, которое может состоять из некоторого числа n блоков. Более того, сообщение вообще не обязано состоять из блоков, в том смысле, что это сообщение не всегда можно разбить на целое число n блоков. В этом случае в разных режимах шифрования приходиться дополнять сообщение различным количеством бит. Такое дополнение почти неизбежно, но минимальная величина, к которой нужно "подтянуть" длину сообщения различна для разных режимов шифрования и напрямую зависит от длины порции сообщения с которой работает каждая итерация алгоритма данного режима. Этот вопрос будет рассмотрен подробнее ниже.

Было бы удобно сразу договориться о некотрых соглашениях, которые будут здесь действовать. Поскольку преобразование данных блочным шифром учитывается здесь лишь как часть алгоритма режима шифрования, то удобно это преобразование рассматривать как функцию, которая получает на входе какие-то данные (будем называть их входнЫми данными) и после их преобразования возвращает выходнЫе данные. Когда блочный шифр применяется в режиме шифрования для зашифрования данных будем обозначать эту функцию

где K – это секретный ключ, на котором работает шифр. Когда же блочный шифр используется в данном режиме для расшифрования будем обозначать эту функцию

. Сами же понятия зашифрование и расшифрование будем применять теперь только к алгоритму режима шифрования в целом. Зашифрованием будем называть процесс преобразования алгоритмом выбранного режима шифрования открытого текста сообщения в шифротекст. Обратный же процесс расшифрования алгоритмом режима шифрования выполняется для восстановления открытого текста сообщения из шифротекста.

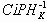
Далее будут рассмотрены пять режимов шифрования так, как они представлены в документе [1], изданном НИСТ США и озаглавленном "Рекомендации для режимов шифрования с блочным шифром". Это отнюдь не единственный документ изданный НИСТ касательно режимов шифрования. До этого был издан документ, описывающий четыре режима для блочного шифра DES, а также другой документ – для тройного DES (Triple DES algorithm или TDEA), в котором описано семь режимов, три из которых являются лишь вариацией на тему тех же режимов, что были описаны для DES. Основным достоинством последнего изданного документа [1] является во-первых то, что его рекомендации относятся к любому, одобренному НИСТ блочному шифру, и во-вторых в нём описан ещё один режим шифрования – пятый. Вот эти режимы:

ECB (Electronic Code Book) – електронная кодовая книга

CBC (Cipher Block Chaining) – сцепление блоков по шифротексту

CFB (Cipher Feed Back) – обратная загрузка шифротекста

OFB (Output Feed Back) – обратная загрузка выходных данных.

CTR (Counter) – шифрование со счётчиком

Электронная кодовая книга

Данный режим является электронным аналогом режима, использовавшегося агентами для отправки зашифрованного сообщения ещё в начале XX века. Агент получал блокнот, каждая страница которого содержала уникальную последовательность – код с помощью которого и зашифровывалось сообщение. После использования такая страница вырывалась из блокнота и уничтожалась. При необходимости сообщение дополнялось так, чтоб на вырываемых страничках не оставалось не использованного кода. Принимающая сторона имела копию блокнота, поэтому, при условии синхронного использования страниц такой режим шифрования обеспечивал как зашифрование так и расшифрование сообщений. В ECB использованию одной страницы кодовой книги при зашифровании соответствует применение к входным данным преобразования функцией

, а при расшифровании -

. Обоим сторонам для того, чтобы синхронизироваться достаточно договориться о значении секретного ключа K . Вобще этот режим является самым простым и первым приходящим на ум способом использования блочного шифра для шифрования сообщений. Он проиллюстрирован на рис.1.

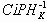
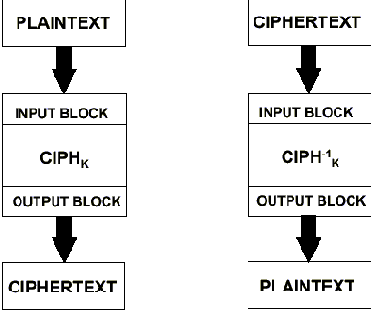
Рис. 1. Режим шифрования електронная кодовая книга – ECB.

Как видно из рисунка весь алгоритм ECB состоит в применении напрямую функций

к сообщению и шифротексту для зашифрования и расшифрования соответственно, что также может быть выражено в виде уравнений:

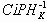
ECB зашифрование:

, где j=1…n

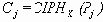
ECB расшифрование:

, где j=1…n

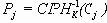
В уравнениях приняты следующие обозначения:

Pj

– очередной, j-ый блок открытого текста (на рисунке – PLAINTEXT).

Cj

– очередной, j-ый блок шифротекста (на рисунке – CIPHERTEXT).

Таким образом шифрование происходит блоками, соответствующими размеру входных/выходных данных для функций

. Блоки шифруются отдельно и независимо друг от друга, что позволяет делать это параллельно. Это достоинство режима ECB и его простота скрадываются двумя значительными недостатками. Первый – то, что длина сообщения должна быть кратна длине блока входных данных блочного шифра, то есть всё сообщение либо можно разбить на целое число таких блоков, либо необходимо каким-то образом дополнять последний блок не несущими информацию данными. Второй недостаток ещё более существенный. Поскольку при зашифровании очередной блок шифротекста полностью определяется только соответствующим блоком открытого текста и значением секретного ключа K, то одинаковые блоки открытого текста будут преобразовываться в этом режиме в одинаковые блоки шифротекста. А это иногда нежелательно, так как может дать ключ к анализу содержания сообщения. Например, если шифруются данные на жёстком диске, то пустое пространство будет заполнено одинаковыми байтами, оставшимися там от форматирования диска. А значит по шифротексту можно будет догадаться о размере полезной информации на диске. 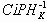В таких случаях нужно применять другие режимы шифрования.

Сцепление блоков по шифротексту

В режиме шифрования CBC происходит "сцепливание" всех блоков сообщения по шифротексту. Как это достигается – видно из рисунка 2, иллюстрирующего этот режим шифрования.

Как видно из рисунка в алгоритме шифрования на вход функции

каждый раз подаётся результат суммирования по модулю 2 открытых данных очередного блока сообщения (на рисунке – PLAINTEXT) и выходных данных (на рисунке – OUTPUT BLOCK) функции

для предыдущего блока. Поскольку выходные данные функции

для очередного блока идут прямо на выход алгоритма CBC, то есть являются шифротекстом этого блока и одновременно поступают на вход этой же функции для зашифрования последующего блока, то говорят, что происходит сцепление блоков по шифротексту. Первый блок открытых данных суммируется с т.н. вектором инициализации, речь о котором пойдёт ниже. Пока же достаточно понимать, что этот вектор инициализации становится известен как отправителю, так и получателю в самом начале сеанса связи (поэтому зачастую его называют просто синхропосылкой). Расшифрование происходит, соответственно, в обратном порядке – сначала к шифротексту применяют функцию

, а затем суммируют с предыдущим блоком шифротекста для получения на выходе алгоритма очередного блока открытого текста. Первый блок открытого текста, опять же, восстанавливается с помощью вектора инициализации. Таким образом весь алгоритм может быть выражен в виде уравнений следующим образом:

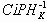
CBC зашифрование:

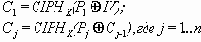
CBC зашифрование:

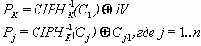
В уравнениях приняты следующие обозначения:

IV

– вектор инициализации (на рисунке – Initialization Vector);

Pj

– очередной, j-ый блок открытого текста.

Cj

– очередной, j-ый блок шифротекста.

Поскольку, как наглядно следует из рисунка, в режиме CBC при зашифровании каждая итерация алгоритма зависит от результата предыдущей итерации, то зашифрование сообщения не поддаётся расспараллеливанию. Однако в режиме расшифрования, когда весь шифротекст уже получен, функции

вполне можно исполнять параллельно и независимо для всех блоков сообщения. Это даёт значительный выигрыш по времени. В этом режиме стоит остановиться ещё на одной детали. Дело в том, что последний блок шифротекста, который получается на выходе алгоритма режима CBC зависит как от ключа блочного шифра и вектора инициализации, так и (что важнее в данном случае) от всех бит отрытого текста сообщения. А это означает, что этот последний блок шифротекста можно использовать как своего рода идентификатор сообщения. Такой идентификатор не даёт постороннему наблюдателю никакой информации о содержимом всего сообщения в целом, и в то же время, практически однозначно определяет его (сообщение). Более того подделать этот идентификатор без знания ключа шифрования K так же трудно, как и правильно угадать сам ключ. Этот идентификатор широко используется для аутентификации сообщений и отправителей и носит название MAC (Message Authentication Code), в русскоязычной литературе – КАС (код аутентификации сообщения).

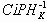
Обратная загрузка шифротекста

В алгоритме режима обратной загрузки шифротектса очередной блок открытого текста суммируется по модулю с блоком предыдущего шифротекста, но только после того, как этот шифротекст подвергнется дополнительной обработке функцией

. Так происходит зашифрование сообщения в этом режиме. Для расшифрования нужно просто суммировать (естественно по модулю 2) очередной блок шифротекста с предыдущим, пропущенным опять-таки через функцию

. Работа шифра проиллюстрирована на рисунке 3. Обратите внимание, что при за- и расшифровании в этом режиме блочный шифр используется только в режиме зашифрования (то есть функции

нет вообще). Такие режимы, в которых функция преобразования блочным шифром применяется до суммирования с блоком открытого текста называют поточными (далее будет видно почему), если же функция преобразования блочным шифром вызывается в алгоритме режима после наложения блока открытого текста, то такой режим шифрования будет блочным.

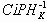
В поточных режимах шифрования можно применить трюк, позволяющий сгладить проблему дополнения последнего блока сообщения. Вместо того, чтобы скармливать алгоритму режима на каждой его итерации сообщение полными блоками, текст подаётся порциями длиной

, где b – длина блока в битах. И далее, при суммировании используется только s старших бит выходных данных функции

, остальные попросту отбрасываются. Следующая итерация режима получает на входе s бит шифротекста, которые сдвигают влево на s бит входные данные функции

, оставшиеся там с предыдущей итерации.

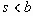
Таким образом, длина всего сообщения теперь должна быть кратна не b а s, что означает меньшее количество бит необходимое для выравнивания сообщения. Варьируя величину s можно изменять скорость работы прогаммы, реализующей режим шифрования CFB. Например, если известно, что пропускная способность канала передачи данных ограничена (или программа выдаёт текст сообщения для зашифрования с определённой скоростью), тогда, с учётом этих ограничений, можно подобрать такое значение s, что пропускная способность канала будет использоваться наиболее эффективно (либо текст сообщения будет обрабатываться с оптимальной скоростью). Но за всё приходиться платить – и теперь, поскольку за одну итерацию алгоритма шифрования преобразуется меньшее число бит, то таких итераций потребуется больше. Отношение

характеризует количество "холостой" работы блочного шифра.

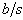
Уравнения режима шифрования CFB приведены ниже:

CFB зашифрование:

-----------------------------------------------------

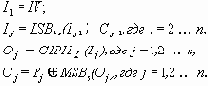
CFB расшифрование:

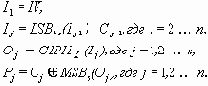
В уравнениях приняты следующие обозначения:

IV

– вектор инициализации;

Pj

– очередной, j-ый блок открытого текста.

Cj

– очередной, j-ый блок шифротекста.

LSBm (

X) - m младших бит (less significant bits) двоичного числа X

MSBm (

X) - m старших бит (most significant bits) двоичного числа X

X

| Y – конкатенция битовых строк, представленных числами X и Y,

напр. 01 | 1011 = 011011

В режиме CFB при зашифровании входные данные для функции

формируются на основании шифротекста с предыдущей итерации алгоритма, поэтому параллельное выполнение итераций алгоритма невозможно. Однако, в режиме расшифрования CFB при условии наличия полного шифротекста все порции открытого текста можно получить одновременно.

Обратная загрузка выходных данных

Режим OFB, как и CFB является поточным, то есть функция

вызывается в алгоритме до суммирования с порцией открытого текста. Но на этот раз на вход

подаётся не шифротекст с предыдущей итерации, а просто её же выходные данные. Иллюстрация режима приведена на рисунке 4. То есть происходит как бы зацикливание функции

. В такой ситуации становится важным однократное использование вектора инициализации. И вот почему. Допустим два различных сообщения шифруются в режиме OFB с использованием одного и того же вектора инициализации. Тогда, если противнику становится известен какой-либо j-ый блок открытого текста первого сообщения, то, имея j-ый блок шифротекста он легко может вычислить Oj – выходные данные

, а поскольку они зависят только от вектора инициализации, который одинаков для обоих сообщений, то можно утверждать, что и во втором сообщении это будет тот же Oj , отсюда, имея j-ый блок шифротекста второго сообщения противник тутже получит открытый текст j-го блока второго сообщения. Поэтому в алгоритме OFB необходимо избегать не только повторения векторов инициализации, но и того, что бы любой j-ый блок входных данных функции

для одного сообщения не использовался как вектор инициализации для другого сообщения.

Ниже приведены уравнения для за- и расшифрования в режиме OFB:

OFB зашифрование:

-----------------------------------------------------

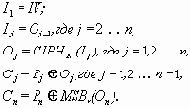
OFB расшифрование:

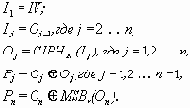
В уравнениях приняты следующие обозначения:

IV

– вектор инициализации;

Pj

– очередной, j-ый блок открытого текста.

Cj

– очередной, j-ый блок шифротекста.

MSBr (

X) - r старших бит (most significant bits) двоичного числа X

Как можно заметить из уравнений – проблема дополнения сообщения для OFB решается просто: её для этого режима просто не существует. Для последнего, возможно неполного, блока сообщения используется ровно столько бит выходных данных функции

, сколько бит в этом блоке. Таким образом в этом режиме, в отличие от предыдущих длина сообщения остаётся неизменной в процессе шифрования и, главное, при передаче.

Шифрование со счётчиком

В потоковом режиме шифрования со счётчиком на каждой итерации алгоритма шифрования на вход функции

подаётся некое случайное значение Т. Эти входные данные должны быть различны для всех итераций алгоритма в которых блочный шифр использует один и тот же ключ шифрования, поэтому генератор таких значений иногда называют счётчиком (что даёт наиболее простой способ генерации уникальных значений T). На самом деле требование уникальности входных данных функции

при определённом значении K будет удовлетворено и в случае использования ГПК (генератора псевдослучайных кодов), но тогда необходим начальный вектор инициализации для ГПК со стороны отправителя и получателя сообщений. Режим шифрования CTR проиллюстрирован на рисунке 5.

Таким образом шифротекст в алгоритме режима CTR получается суммированием по модулю 2 очередного блока открытого текста с выходными данными функции

. На вход функции

подаётся очередное значение Tj счётчика блоков сообщения. Расшифрование происходит также путём суммирования по модулю 2 очередного блока шифротекста и результата преобразования функцией

очередного значения счётчика Tj. Обе операции за- и расшифрования в режиме CTR можно производить параллельно и независимо для всех блоков. Кроме того в этом режиме также отсутствует проблема последнего блока. Это видно из уравнений режима CTR:

CTR зашифрование:

---------------------------------------------------

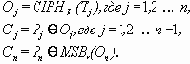
CTR расшифрование:

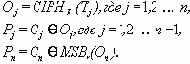
В уравнениях приняты следующие обозначения:

Pj

– очередной, j-ый блок открытого текста.

Cj

– очередной, j-ый блок шифротекста.

MSBr (

X) - r старших бит ( most significant bits) двоичного числа X

Режим CTR обладает всеми достоинствами режима ECB (параллельное исполнение, простота и возможность непосредственного за- и расшифрования любого блока сообщения по отдельности и независимо от других блоков). Но кроме того, режим CTR исправляет все недостатки шифрования в режиме электронной кодовой книги: одинаковые блоки открытого текста теперь уже не будут преобразованы в одинаковые блоки шифротекста; отпадает необходимость дополнения последнего блока шифротекста. К тому же в этом режиме (как в любом поточном режиме) используется только функция зашифрования

, а для некоторых блочных шифров (например для AES – нового американского стандарта блочного шифра), это даёт некоторый выигрыш в производительности. Вот почему этот режим зачастую является наиболее эффективным.

Вектор инициализации

В таких режимах шифрования, как CBC, CFB и OFB на вход функций

подаётся вектор инициализации (IV). Причём как отправитель, так и получатель в начале сеанса связи должны иметь один и тот же IV. Значение IV вовсе не обязано быть секретным и вполне может быть передано вместе с первым блоком шифротектса. Что действительно важно, так это то, что в режимах CBC и CFB это значение должно быть непредсказуемым, а в режиме OFB – уникальным.

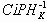
Непредсказуемости

в режимах CBC и CFB можно достичь несколькими способами. Например, можно подвергнуть преобразованию той же функцией

значение какого-либо счётчика (скажем счётчика сообщений). Или использовать ГПК для генерации псевдослучайной последовательности нужной длины.

В режиме OFB вектор инициализации не обязан быть непредсказуемым, зато он должен быть уникален для всех сеансов связи в которых в OFB используется один и тот же секретный ключ шифрования K. Этого можно достичь опять же используя счётчик сообщений. Если же не следовать этому требованию, то секретность сообщения в режиме OFB может быть легко скомпрометирована. Пример приведён выше при описании самого режима OFB. Одним из следствий этого требования является то, что очередной вектор инициализации для режима OFB нельзя генерировать путём применения функции

с тем же ключём K.

Накопление ошибок в различных режимах шифрования

Прежде всего – что такое ошибка. Ошибкой в бите данных будем называть подмену бита со значением "1" на бит "0" и наоборот. Далее обсудим как такая ошибка может повлиять на результат применения алгоритма шифрования в различных режимах, когда она возникает в шифротексте, векторе инициализации или значении счётчика Tj в режиме CTR.

В любом режиме ошибка в пределах блока (или порции – для CFB) шифротекста ведёт к неправильному расшифрованию этого блока. Так, в режимах CFB, OFB и CTR ошибочным на выходе будет тот же бит, остальные биты останутся невредимыми. В режимах же ECB и CBC повреждённым, в зависимости от силы преобразования используемого блочного шифра, может стать любой бит с вероятностью повреждения

.

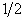
В режимах ECB, OFB и CTR ошибка в бите отдельного блока шифротекста на повлияет на другие блоки при расшифровании. В режиме CBC такая ошибка приведёт к ошибке в том же бите при расшифровании следующего блока сообщения. Остальных блоков эта ошибка не коснётся. Другое дело режим CFB: здесь ошибка в одном бите порции шифротекста распространится на

следующих порций шифротекста (b – длина блока входных данных функции

; s – длина порции шифротекста). К тому же при расшифровании измениться с вероятностью

теперь может любой бит этих

порций.

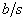
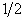
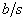
В режиме CTR ошибка в бите счётчика Tj приведёт к возможности изменения любого бита соответствующего блока шифротекста с вероятностью

.

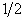
Ошибка в бите вектора инициализации также повлияет на результаты расшифрования. Так, в режиме OFB ошибка в одном бите вектора инициализации при расшифровании приведёт к полностью неверным результатам. В режиме же CFB эта ошибка при расшифровании заденет как минимум первую порцию сообщения, а как максимум

(где b,s – то же, что раньше, а i – номер ошибочного бита слева) порций сообщения. Для обоих этих режимов повреждённым в затронутых блоках (порциях для CFB) может оказаться любой бит с вероятностью

. В режиме CBC ошибка в бите вектора инициализации приведёт к неправильному расшифрованию лишь первого блока, да и то ошибочным окажется только один бит – остальные останутся неповреждёнными. Отсюда следует, что режим CBC подвержен нарушению защиты в случае преднамеренного изменения бита в векторе инициализации с целью изменить содержание сообщения. Поэтому в этом режиме необходимо обеспечить целостность вектора инициализации. Режимы OFB и CTR также подвержены нарушению целостности сообщения, но для них это становится возможным уже при преднамеренном изменении бита любого блока шифротекста. Поэтому в этих режимах должна быть обеспечена целостность блоков шифротекста при передаче. То же касается и режима CFB, хотя в этом режиме для любой порции шифротекста (кроме последней) нарушение её целостности может быть обнаружено по возникновению ошибок при расшифровании последущих порций шифротекста.

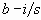
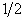
Таблица отражает эффект распространения ошибки во всех пяти режимах шифрования.

Эффект распространения ошибки

Режим шифрования

Эффект от ошибки в бите шифротекста

Эффект от ошибки в i-том бите вектора инициализации IV

ECB

ОЛБ при расшифровании блока

Не используется

CBC

ОЛБ при расшифровании блока

ООБ при расшифровании блока

CFB

ООБ при расшифровании блока

ОЛБ при расшифровании блоков

OFB

ООБ при расшифровании блока

ОЛБ при расшифровании блоков

CTR

ООБ при расшифровании блока

Ошибка в счётчике

ведёт к ОЛБ при расшифровании блока

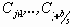
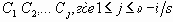
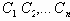
В таблице приняты следующие сокращения:

ОЛБ – ошибка в любом бите, то есть повреждённым при расшифровании с вероятностью

может оказаться любой бит блока (или порции).

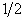
ООБ – ошибка в одном бите, то есть при расшифровании повреждается один бит, находящийся в той же позиции, что и бит вызвавший ошибку.

Вставка или удаление одного бита в блок (или порцию) шифротекста нарушает синхронизацию за- и расшифрования, что приводит к возможности появления ошибок при расшифровании во всех битах, начиная с ошибочного. Только в режиме CFB с размером порции сообщения обрабатываемой за одну итерацию алгоритма в 1 бит синхронизация восстановиться автоматически через

итераций алгоритма. Во всех остальных режимах синхронизацию необходимо будет восстанавливать непосредственно.

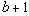
Список использованной литературы

Recommendation for Block Cipher Modes of Operation. NIST Special Publication 800-38A. Technology Administration U.S.Department of Commerce. 2001 Edition

Защита информации в компьютерных системах и сетях. Под ред. В.Ф.Шаньгина.-М.:Радио и связь, 1999.-328с.

Communication theory of secrecy systems. C.E.Shennon.Bell System Technical Journal, vol.28, 1949.

Страничка классических блочных шифров. А.Винокуров.

Введение в криптографию. Под общ. ред. В.В.Ященко.-M.: МЦНМО: "ЧеРо", 2000.

Содержание раздела