Инверсная (обратная) машина
Определение. 7 Инверсия iM – машина, которая, если она принимает выход машины Мi, то, после конечной задержки, выдает входную последовательность Мi.
Разумеется, определенную выше инверсию iM можно построить только, если Мi информацию сохраняющая и имеет конечную память.
В качестве примера, возьмем машину Table 6а, которая информацию сохраняющая первого порядка. При любом начальном состоянии и любой выходной последовательности, знания начального состояния и первого выходного символа достаточно, чтобы определить первый входной символ. Отсюда видно, что такая машина не имеет задержки при декодировании.
|
PS |
NS,z | ||||
|
x=0 |
x=1 | ||||
|
A |
C,1 |
D,0 | |||
|
B |
D,0 |
A,1 | |||
|
C |
D,1 |
B,0 | |||
|
D |
C,0 |
B,1 | |||
PS
NS,x
z=0
z=1
A
D,1
C,0
B
D,0
A,1
C
B,1
D,0
D
C,0
B,1
a)
b)
Table 6
В Table 6b показана инверсная таблица, которая построена, как выходная таблица переходов.
Рассмотрим один из способов восстановления входной последовательности.
Для каждой машины, которая сохраняет информацию µ-порядка, знания состояния в момент t-µ+1 и последних µ
выходных символов последовательности
zt-?+1,zt-?+2,z, … zt достаточно для однозначного определения выходного символа xt+?+1.
Следовательно, если мы передадим выходную последовательность машине Мi µ-порядка на входы регистра, который состоит из µ-1
элементов задержки, мы можем построить комбинационную схему, которая принимает содержимое регистра, так же, как состояние машины Мi
в момент t-µ+1 и вырабатывает значение xt+?+1.
Комбинаторный блок можно задать в виде таблицы истинности, в которой величина xt+?+1 определяется для каждой возможной комбинации из S(t-µ+1) и
zt-?+1,zt-?+2,z, … zt. Информация относительно состояния Мi. может быть передана комбинационной схеме копией оригинальной машины Мi, которая может быть установлена при t=µ-1 в то же самое состояние, в котором Мi
была при t=0, и принято как ее задержанные (при µ-1 задержках) версии входов М. Структурная схема такой декодирующей системы показана на Рис. 7.
Приведенная декодирующая система не совсем экономна, так как требует копии исходной машины и (µ-1)-разрядного регистра ([8]).
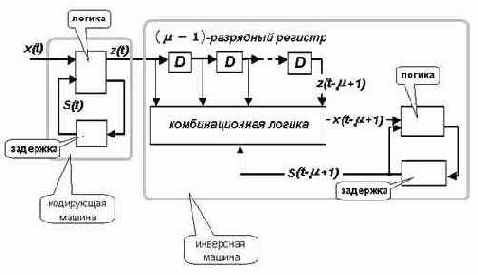
Рис. 7