Схема цифровой подписи на основе блочного шифра.
Ниже приведены числовые параметры и используемые вспомогательные алгоритмы рассматриваемой схемы цифровой подписи:
- EK – алгоритм зашифрования с размером блока данных и ключа n и nK битов соответственно;
- Гm(s,K) – алгоритм выработки m битов криптостойкой гаммы с использованием n-битового вектора начальных параметров (синхропосылки) s и nK–битового ключа K, представляет собой рекуррентный алгоритм выработки n-битовых блоков данных и их последующего зашифрования по алгоритму EK;
- Pm®nK – набор функций расширения m-битовых блоков данных до nK-битовых для различных m (типично – для кратных n, меньших nK);
- L – фактор количества подписей (система рассчитана на N=2L подписей);
- nT – число битов в подписываемых битовых группах, тогда число групп равно .

- T – подписываемый – n-битовый хэш-блок массива данных;
- KS
– ключ подписи – nK-битовый массив данных; - i – порядковый номер подписи.
- T – подписанный – n-битовый хэш-блок массива данных;
- s – подпись хэш–блока, состоит из массива X, содержащего 2nG n- битовых элементов подписи битовых групп, и массива D, содержащего L n-битовых хэш–комбинаций;
- i – порядковый номер подписи.
Ниже изложены алгоритмы схемы подписи:
1. Алгоритм формирования ключей подписи и проверки подписи.
(a) Формирования ключа подписи.
Ключ подписи формируется как nK-битовый блок данных с помощью аппаратного генератора случайных кодов или криптостойкого программного генератора псевдослучайных кодов KS=GnT(...). Биты ключа должны быть независимы и с равной вероятностью принимать оба возможных значения – 0 и 1.
(b) Формирования ключа проверки подписи. Схема алгоритма формирования ключа проверки подписи изображена на рисунке 4.
Øàã 0. Исходные данные алгоритма – nK–битовый массив данных KS
– ключ подписи.
Øàã 1. Вычисляем nG – количество nT-битовых групп в подписываемых блоках.
Следующие шаги 2–9 выполняются столько раз, на сколько подписей рассчитана схема, т.е. для каждого номера подписи системы.
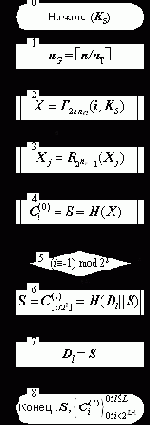 Рис. 4. Алгоритм выработки ключа проверки подписи. |
Øàã 2. Выработать блок гаммы размером 2nnG бит с помощью генератора криптостойкой гаммы на ключе KS с начальным заполнением i (номером подписи) и поместить его в 2nnG–битовый массив X.
Øàã 3. 2nnG–битовый массив X интерпретируется как массив из 2nG n-битовых элементов Xj, X=(X1,X2,...,X2nG), |Xj|=n,
затем для каждого элемента этого массива вычисляется результат его «односторонней прокрутки» 2nT–1 раз.
Øàã 4. Для массива X вычисляется и записывается в блок данных S его хэш-код, который является индивидуальной проверочной комбинацией для подписи номер i.
Следующие шаги 5,6 выполняются количество раз, равное фактору количества подписей L.
Øàã 5. Если l младших бит номера подписи – единицы, переход к шагу 6, иначе – выполнение цикла прекращается и управление передается на шаг 7.
Øàã 6. Текущая хэш-комбинация S объединяется c текущей õýø-êîìáèíàцией Dl уровня l, и для полученного массива вычисляется хэш–значение, которое становится новой текущей хэш–комбинацией.
Øàã 7. Текущая хэш-комбинация S заменяет õýø-êîìáèíàцию Dl уровня l.
Øàã 8. Последняя вычисленная при выполнении алгоритма текущая хэш-комбинация S и будет являться результатом работы алгоритма – ключом проверки подписи. Кроме того, в ходе выполнения алгоритма будут последовательно выработаны хэш-комбинации всех уровней от 0 до L

2. Алгоритм подписи хэш-блока массива данных.
Схема алгоритма подписи хэш-блока массива данных изображена на рисунке 5.
Øàã 0. Исходные данные алгоритма:
Øàã 1. Вычисляем nG – число nT-битовых групп в подписываемом n-битном хэш-блоке.
Øàã 2. Выработать блок гаммы размером 2nnG бит с помощью генератора криптостойкой гаммы на ключе KS с начальным заполнением i (номером подписи) и поместить его в 2nnG-битовый массив X.
Øàã 3. 2nnG-битовый массив X интерпретируется как массив из nG пар n-битовых элементов X=((X1,X2),...,(X2nG–1,X2nG)), |Xj|=n,
затем для каждой составляющей каждого элемента этого массива, соответствующего определенной битовой группе хэш-блока, нужное число раз выполняется процедура «односторонней прокрутки».
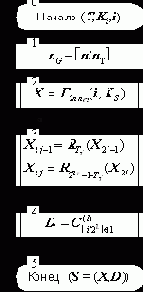 Рис. 5. Алгоритм подписи хэш-кода сообщения. |
Øàã 5. В результате получаем цифровую подпись хэш-блока сообщения S=(X,D), состоящую из массива подписей битовых групп блока X=(X1,X2,...,X2nG) и из массива дополнительных проверочных комбинаций D=(D0,D1,...,DL–1), необходимых для выполнения процедуры проверки подписи и используемых при вычислении попарных проверочных комбинаций.
3. Алгоритм проверки подписи хэш-блока массива данных.
Схема алгоритма проверки подписи хэш-блока массива данных изображена на рисунке 6.
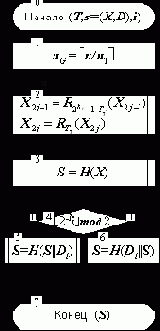 |
Øàã 1. Вычисляем nG – число nT–битовых групп в подписываемом хэш–блоке, имеющем размер n бит.
Øàã 2. В соответствии с правилами проверки подписи производится «односторонняя прокрутка» элементов подписи битовых групп, содержащихся в массиве X, по два элемента на каждую группу.
Øàã 3. Для массива X вычисляется и записывается в S его хэш-код, который должен быть равен индивидуальной проверочной комбинацией для i-той подписи.
Следующие шаги 4–6 выполняются количество раз, равное фактору количества подписей L.
Øàã 4. Производится выбор по значению l-того бита (нумерация с 0 со стороны младшего бита) номера подписи.
Øàã 5. Если значение бита равно 0, то к коду справа добавляется очередная хэш-комбинация, содержащаяся в подписи, для полученного блока вычисляется хэш-функция, которая замещает предыдущее содержимое S.
Øàã 6. Если значение бита равно 1, то выполняется то же самое, только хэш-комбинация добавляется к коду слева.
Øàã 7. В конце выполнения алгоритма в S содержится код, который должен быть сравнен с ключом проверки подписи, если коды одинаковы, подпись считается верной, иначе – неверной.
Заключение.
Стойкость предложенной схемы цифровой подписи определяется стойкостью использованного блочного шифра, а устойчивость ко вскрытию переборными методами –наименьшим из чисел n, nK. Ключевой комплект в данной схеме рассчитан на определенное число подписей, что, с одной стороны, может восприниматься как недостаток схемы, но с другой позволяет лицензировать количество подписей, облегчая тем самым ее коммерческое использование. Рассматриваемая схема подписи не соответствует стандарту России на цифровую подпись, а алгоритм вычисления MDC – стандарту на выработку хэш-кода массива данных, что делает невозможным аттестацию в соответствующих организациях устройств и программных продуктов, их реализующих. Однако изложенные схемы вполне могут быть использованы там, где спорные вопросы не могут быть вынесены на уровень арбитражных и судебных разбирательств, например, в системах автоматизации внутреннего документооборота учреждений, особенно если электронный документооборот не заменяет бумажный, а существует в дополнение к нему для ускорения прохождения документов.
В качестве приложения к настоящей статье приведены исходные тексты на языке ассемблера для процессоров клона Intel 8086 функции вычисления MDC для блоков данных и функции, реализующие алгоритмы описанной схемы цифровой подписи. Функция выработки хэш-кода (MDC) написана таким образом, что позволяет обрабатывать блоки данных по частям, то есть за несколько вызовов. Все функции используют в качестве основы алгоритм зашифрования по ГОСТ 28147–89. Также прилагаются тексты тестовых программ на языке Си для проверки неизменности файлов на основе MDC и цифровой подписи.
Литература.
1. А.Ю.Винокуров. ГОСТ не прост...,а очень прост, М., Монитор.–1995.–N1.
2. А.Ю.Винокуров. Еще раз про ГОСТ., М., Монитор.–1995.–N5.
3. А.Ю.Винокуров. Алгоритм шифрования ГОСТ 28147-89, его использование и реализация для компьютеров платформы Intel x86., Рукопись, 1997.
4. А.Ю.Винокуров. Как устроен блочный шифр?, Рукопись, 1995.
5. М.Э.Смид, Д.К.Бранстед. Стандарт шифрования данных: прошлое и будущее. /пер. с англ./ М., Мир, ТИИЭР.–1988.–т.76.–N5.
6. Системы обработки информации. Защита криптографическая. Алгоритм криптографического преобразования ГОСТ 28147–89, М., Госстандарт, 1989.
7. Б.В.Березин, П.В.Дорошкевич. Цифровая подпись на основе традиционной криптографии//Защита информации, вып.2.,М.: МП "Ирбис-II",1992.
8. W.Diffie,M.E.Hellman. New Directions in cryptography// IEEE Trans. Inform. Theory, IT-22, vol 6 (Nov. 1976), pp. 644-654.
9. У.Диффи. Первые десять лет криптографии с открытым ключом. /пер. с англ./ М., Мир, ТИИЭР.–1988.–т.76.–N5.
[1]
Протоколов в криптографии называется набор правил и алгоритмов более высокого порядка, регламентирующих использование алгоритмов низшего порядка. Его основное назначение – гарантировать правильное использование криптографических алгоритмов.